CAEの構造解析の妥当性の判断や手計算で強度を推定することができるようになり、場合によっては不要な外注委託費用を削減し、必要なところに外注委託費用を回すことができます。
「今、CAEの外注委託先を考えはじめた」「今後CAEを設計に取り入れていこうと考えている」という方には「CAEの構造解析を外注委託するか否か」を考える上で参考になると思います。
「CAE受託ドットコム」は、CAE歴20年の管理人が自身の経験を元にCAEの有効な活用方法を発信するブログです。
下記に関連する内容でお困りごとがあればお問い合わせフォームに質問事項をご連絡頂ければ、時間があるときに回答させて頂きます。リクエストなどにも対応していきたいと思います。
CAEの強度計算で見るべき重要ポイント
強度計算で見るべき重要ポイントは下記の3つです。
- 想定荷重に対して最大何mm、あるいは何cm変形するか?
- 想定荷重に対して最大何[MPa]の応力が発生するか?
- 変形および発生応力のオーダー感に間違いが無いか?
CAEの強度解析結果の妥当性を判断する上で、変形量、発生応力に数%程度オーダーの精度を求める必要はありません。重要なのはこれらのオーダー感に間違いが無いかをチェックすることが大切です。
したがって、複雑な理論式を用いるのではなく簡単な計算式で大体の値を推定し、如何に手間をかけないかが重要です。
ここで言う変形量とは下図のような片持ちはりで言うとはりの先端のわたみ量δ、発生応力とは片持ちはりに発生する応力が最大となる固定部の応力のことを意味します。

変形量と応力の推定方法のポイント
変形量と応力の推定方法のポイントについて解説します。本記事の単位系はmmのSI単位系で下記に記載します。
- はりの計算式にあてはめて変形量と応力を計算
- はりの計算式の中から適切な条件(ピン、固定、フリー)を選定
- 材質を選定(ヤング率E[MPa])
- はりの断面特性を選定(断面2次モーメントI[mm4]、断面係数Z[mm3])
- オーダー感を掴むという意識で大胆な近似
はりの変形量と応力
図1の先端に集中荷重を受ける片持ちはりのはりの変形量(たわみ量)と応力は下記で計算できます。
- はり先端のたわみ量δ = PL3/3EI
P:集中荷重[N]、L:はりの長さ[mm]、E:ヤング率[MPa]、I:断面2次モーメント - はり固定部の応力σ = M/Z = PL/Z
M:はりの固定部に作用するモーメント[N・mm]、Z:断面係数[mm3]
下記を例にはりのたわみ量とはりの固定部の応力を計算してみましょう。下記のようにたわみ量δとはりの固定部の応力σは簡単に計算できます。断面2次モーメントIと断面係数Zは別途解説します。
はりの先端に集中荷重を受ける片持ちはりの場合は、上記の計算式で計算可能です。その他にも下記のような場合で計算式が異なるので、評価対象物がどの条件に近いのかを見極めることが重要です。
適切な条件(ピン、固定、フリー)
- 両端固定の集中荷重
- 両端固定の分布荷重
- 両端ピン支持の集中荷重
- 両端ピン支持の分布荷重
などの支持条件、荷重負荷条件違いによって計算式が異なります。
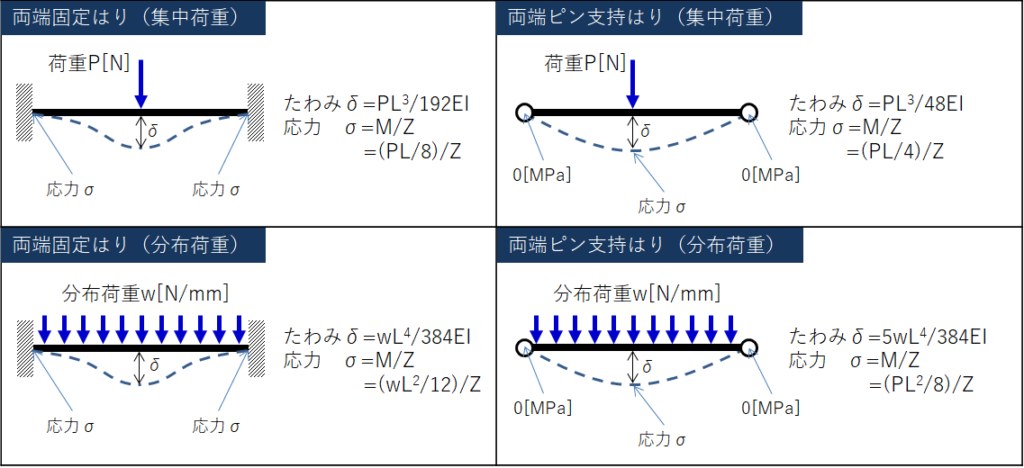
上記以外にも計算式は多数ありますが、どこかの機会で一覧を作成したいと思います。
材質
材質の選定について下記に示します。材料の硬さを示すパラメータのヤング率です。
- 炭素鋼(SS400など):E=206,000[MPa]
- ステンレス鋼(SUS304):E=193,000[MPa]
- 純アルミ(A1085):E=69,000[MPa]
- アルミ合金(A2024):E=74,000[MPa]
はりの断面特性
はりの断面特性について解説します。断面特性とは下記の2つを意味します。断面2次モーメントIは、はりの変形し辛さを表すパラメータ、断面係数Zは、はりの応力の発生し辛さを表すパラメータです。
- 断面2次モーメントI[mm4]
- 断面係数Z[mm3]
上記2つのパラメータは方向によって異なる点に注意が必要です。最も簡単な矩形断面を事例に計算してみます。
- 断面2次モーメントI[mm4]=BH3/12
幅B[mm]、高さH[mm] - 断面係数Z[mm3]=I/(H/2)
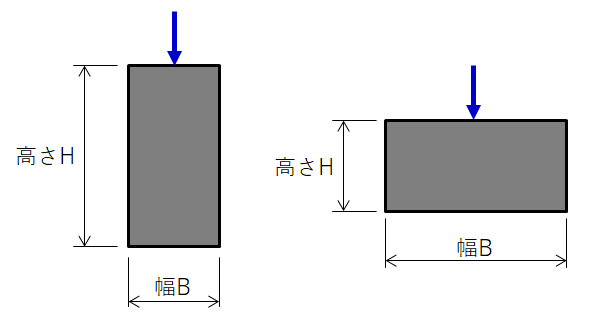
図3 矩形断面
矩形断面の断面特性(上下方向)
幅B=100[mm]、高さH=200[mm]
断面2次モーメントI=BH3/12
=100×2003/12
=66,666,667[mm4]
断面係数Z=I/(H/2)=66666667/(200/2)
=666,667[mm3]
矩形断面の断面特性(左右方向)
幅B=200[mm]、高さH=100[mm]
断面2次モーメントI=BH3/12
=200×1003/12
=16,666,667[mm4]
断面係数Z=I/(H/2)=16666667/(100/2)
=333,333[mm3]
上記のように断面2次モーメントI、断面係数Zは方向によって異なることが確認できました。上下方向のほうが変形し辛いので断面2次モーメントIの値は大きくなり、上下方向のほうが強度的に強いので断面係数Zは大きくなっています。
次は、I鋼、H鋼についても同様に断面2次モーメントI、断面係数Zを計算してみます。
- 断面2次モーメントI[mm4]=BH3/12-(B-t)(H-2t)3/12
幅B[mm]、高さH[mm]、厚みt[mm] - 断面係数Z[mm3]=I/(H/2)
- 断面2次モーメントI[mm4]=2tH3/12+(B-2t)t3/12
幅B[mm]、高さH[mm]、厚みt[mm] - 断面係数Z[mm3]=I/(H/2)

図3 形鋼断面
I形断面の断面特性(上下方向)
幅B=100[mm]、高さH=200[mm]
厚みt=10[mm]
断面2次モーメントI
=BH3/12-(B-t)(H-2t)3/12
=100×2003/12-(100-10)(200-2×10)3/12
=22,926,667[mm4]
断面係数Z=I/(H/2)=22926667/(200/2)
=229,267[mm3]
H形断面の断面特性(左右方向)
幅B=200[mm]、高さH=100[mm]
厚みt=10[mm]
断面2次モーメントI
=2tH3/12+(B-2t)t3/12
=2×10×1003/12+(200-2×10)×103/12
=1,681,667[mm4]
断面係数Z=I/(H/2)=1681667/(100/2)
=33,633[mm3]
上記のように断面2次モーメントI、断面係数Zは方向によって大きく異なりますね。断面2次モーメントで約14倍、断面係数で約7倍。すなわち、たわみ量が14倍、発生応力が7倍異なることを意味します。I形鋼、H形鋼の設置方向には注意が必要ですね。
オーダー感を掴むための大胆な近似
実際の構造物は、上記のような条件に必ずしもあてはまらず下記のような場合が多いです。
- はり断面が一様断面ばかりでは無い
- 固定部が固定とピン支持の間のような支持条件
- 荷重分布が一様では無い
条件が違えば全く予測できないかと言えばそうではありません。CAEの精度検証を行う上で重要なことは、オーダー感が合っていることを確認することです。下記の事例について手計算とCAEの結果と比較してみましょう。
たわみ量の検証

図4に示すはりの断面形状が固定部から先端へ連続的に変化する片持ちはりに1[N/mm2]の圧力荷重を負荷した場合のたわみ量を手計算で算出します。
ここで重要なのは短時間でCAEの結果のオーダー感の検証する、あるいは強度設計において最適な形状を検討することなのでたわみ量の計算は、図4に示すような近似を行います。
はりのたわみ量は、はり全体が少しずつたわみが生じた結果としてはりの先端のたわみ量が決まります。
したがって、近似する断面は固定部と先端の平均断面とします。では、実際に近似したはりのわたみ量を計算してみます。
- はりの断面を一様断面に近似
- たわみ量を計算をするときのはりの断面は、はり全体の平均断面を使う
たわみ量δ = wL4/8EI = 1307×79004/(8×206000×3.527×1011) = 8.8[mm]
単位長さ当たりの荷重w = 圧力[N/mm2]×荷重負荷面積A[mm2]/L[mm]
= 1×10325300/7900 = 1307[N/mm]
荷重負荷面積A = 台形の面積 = (694+1920)×7900/2=10325300[mm2]
断面2次モーメントI= BH3/12 = 1307×1479.53/12 = 3.527×1011[mm4]
ヤング率E = 206000[MPa]
たわみ量δ=8.8[mm]が計算できました。
ここで注意したいのはこの数値は、平均的な一様断面の計算結果であるため、下記理由により実際のたわみ量δは8.8[mm]より小さくなるはずであるという点です。
- 実際の断面形状は、はり固定部が太く、先端が細い(→近似したはりよりもたわみが小さくなる)
- 実際の負荷荷重は、はり固定部の荷重が大きく、先端の荷重は小さい(→近似したはりよりもたわみが小さくなる)
次にFEMの計算をしてみます。図5に示す境界条件は、はりの固定部を拘束し、はりの上面に圧力荷重1[N/mm2]を負荷しました。
図6に図5の条件で計算した結果を示します。図6に示すようにはりのたわみ量ははりの先端で最大となり、はり先端のたわみ量は3.2[mm]であることが分かります。
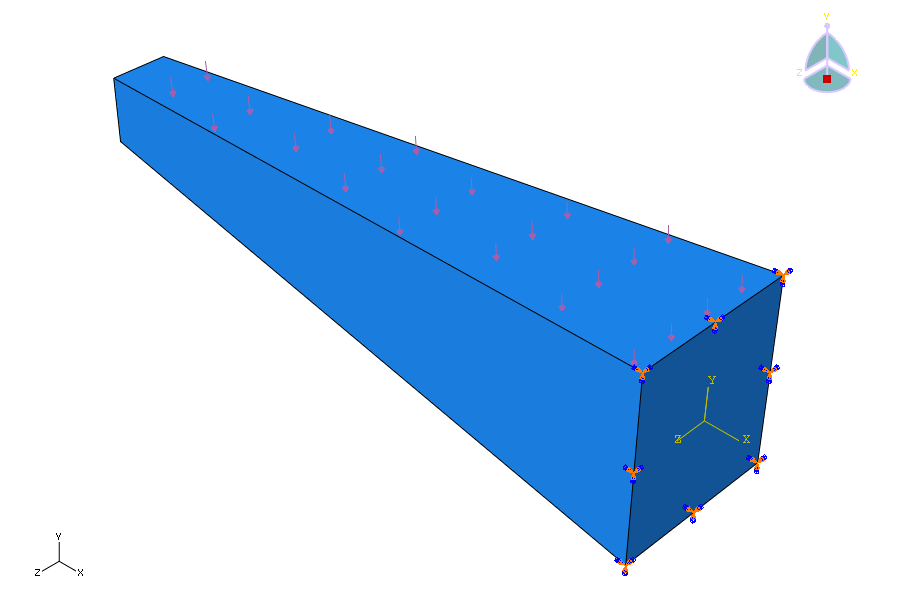

ここで、手計算のたわみ量δは8.8[mm]に対し、CAEのたわみ量δは3.2[mm]であることが分かりました。今回の検討で分かることは、
- 手計算とCAEのオーダー感は一致している
- 手計算のたわみ量より、CAEのたわみ量は小さい
ということが分かり、CAEの結果が妥当であると判断できます。
もっと大胆な近似をした場合は手計算とCAEの結果にズレが大きくなることもあるかと思いますが、近似度合いによってその妥当性の判断をその都度行って下さい。
応力の検証

次は先ほどの同様の片持ちはりで応力を計算してみましょう。たわみ量δの計算では、はり全体の平均断面を近似断面として使用しましたが応力を計算する場合は、応力を知りたい箇所の断面を使います。
したがって、図7に示すような近似により応力を計算します。図7に示した応力σの計算式は、はりの固定部の応力を求める計算式なので、今回の場合ははりの固定部の断面を使います。
では、実際に近似したはりの応力を計算してみます。
- はりの断面を一様断面に近似
- 応力を計算をするときのはりの断面は、応力を知りたい箇所の断面を使う
応力σ = M/Z = (wL2/2)/Z = 1307×79002/1.479×109 = 28[MPa]
単位長さ当たりの荷重w = 圧力[N/mm2]×荷重負荷面積A[mm2]/L[mm]
= 1×10325300/7900 = 1307[N/mm]
荷重負荷面積A = 台形の面積 = (694+1920)×7900/2=10325300[mm2]
断面係数Z = I/(H/2) = 1.590×1012/(2150/2) = 1.479×109[mm3]
断面2次モーメントI= BH3/12 = 1920×21503/12 = 1.590×1012[mm4]
応力σ=28[MPa]が計算できました。ここで注意したいのはこの数値は、平均的な一様断面の計算結果であるため、下記理由により実際の応力σは28[MPa]より小さくなるはずであるという点です。
- 実際の負荷荷重は、はり固定部の荷重が大きく先端の荷重は小さい(→近似したはりよりもモーメントが小さくなる)
次にFEMの計算をしてみます。図8に示す境界条件は図5と同様に、はりの固定部を拘束し、はりの上面に圧力荷重1[N/mm2]を負荷しました。
図9に図8の条件で計算した結果を示します。図9に示すようにはりの固定部の応力ははりの固定部で最大となり、上面側で引張応力19[MPa]、下面側で圧縮応力19[MPa]であることが分かり、曲げ応力として19[MPa]の応力が生じています。
※Abaqus student edition(要素数上限1,000)なので要素分割粗いですがその点ご勘弁下さい。

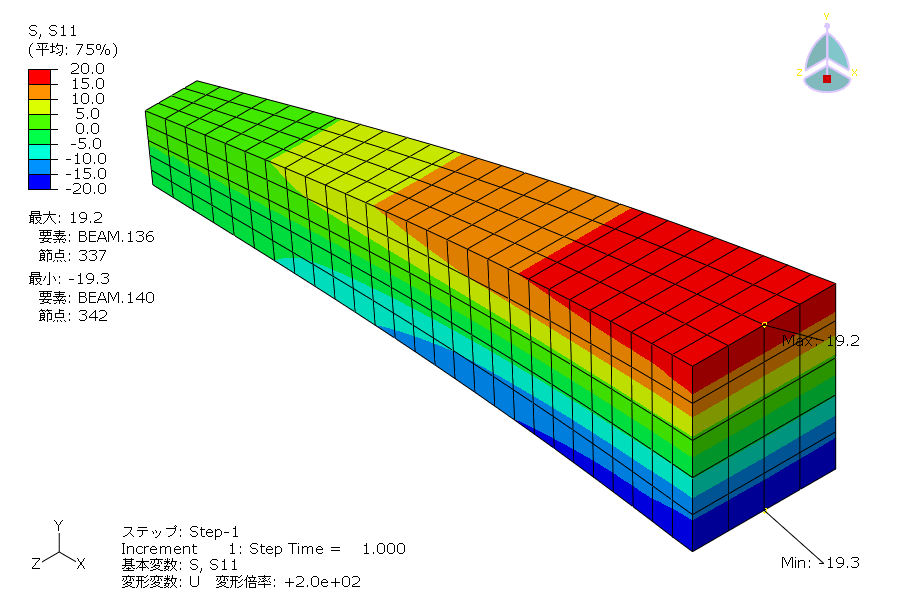
ここで、手計算の応力σは28[MPa]に対し、CAEの応力σは19[MPa]であることが分かりました。今回の検討で分かることは、
- 手計算とCAEのオーダー感は一致している
- 手計算の応力より、CAEの応力は小さい
ということが分かり、CAEの結果が妥当であると判断できます。
手計算でCAEの検証や設計検討をする際は、安全側(想定荷重は実際より大き目)に見ておくと設計の手戻りが減らせる可能性が高くなりますね。
設計にどこまで手計算が活用できるのか
上記事例のように形状をはりで近似でき、部材に作用する負荷荷重が明確に分かるものについては手計算はかなり有効であることを上記で示せたと思います。
エクセルで計算式を作ってしまえばCAEで検討するより効率的に設計が進むと思います。
今回は、はりの計算の一部をご紹介しましたが今後はその他の手計算事例も紹介していきたいと思います。
また、従来の量産設計品などでCAEの結果があるものについては、従来品に対して新規設計品の断面係数をどう変更すれば応力がどうなるかは概ね予測できます。
次に、設計するにあたって、手計算よりCAEのほうが効率が良い場合を考えます。
以下のようなケースは手計算の方法をどうするかで時間と頭を使うより、CAEで検討したほうが効率的です。頭と時間は有効に使いたいですよね。
余談ですが、自身の経験として手計算をひたすら強いられストレスマックスに。今となっては貴重な経験ですが。。。。
- 構成部品が多数あり各部材に作用する荷重が分からない
- 負荷荷重が複雑で色んな方向の荷重を考慮しないといけない
- 構成部品が多数あり応力が最大になる箇所の予想がつきにくい
- 部品に複雑な形状があり応力集中を考慮する必要がある
構成部品が多数あり各部材に作用する荷重が分からない
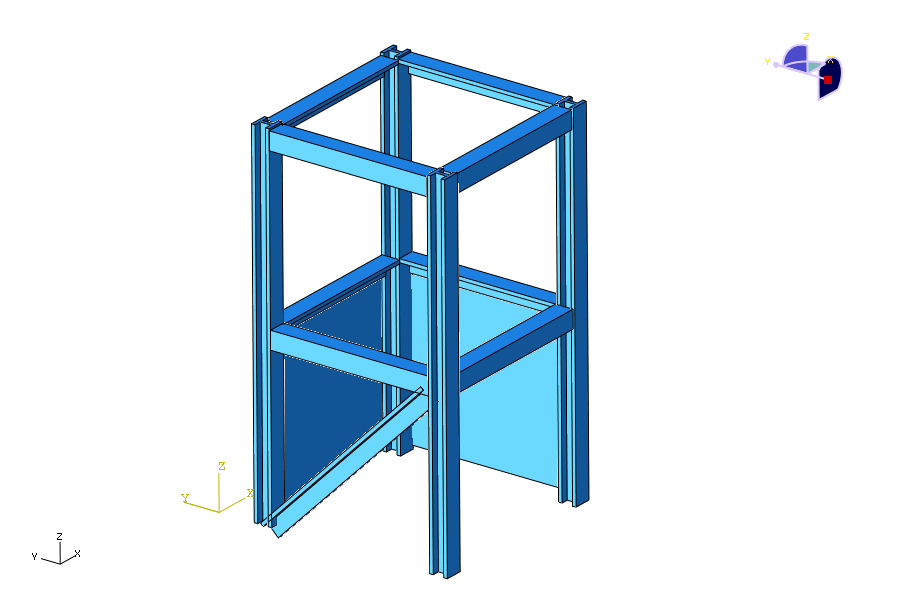
図10のような事例の場合、H鋼、Lアングル、T字鋼、パネルで構成されています。
この場合、外力としての負荷荷重が入力されると、各部材で荷重を分担することになります。
そうなると、どの部材が何[kN]をどの方向に分担するのかを計算する必要があります。
これを手計算するとなると非常に手間です。CAEで計算すると短時間で簡単にたわみ、応力を計算することができます。
負荷荷重が複雑で色んな方向の荷重を考慮しなければならない

図11のように自重と複雑な水圧荷重を考慮しなければならない場合も手計算で計算しようとすると時間がかかってしまいます。
図11の事例以外にも複数の集中荷重が作用する場合は各荷重ケースについて計算する必要があるため、手計算に時間がかかってしまい非常に非効率です。
手計算よりCAEのほうが素早くアウトプットできる場合はCAEで検討することをおすすめします。
構成部品が多数あり高応力が生じる箇所の予想がつきにくい
図10の事例で地震荷重が入力された場合を考えると、最弱部がH鋼、斜材のT字鋼、パネルなのかが即座に分かりません。
その場合、少なくともH鋼、斜材のT字鋼、パネルについて手計算で応力を算出する方法について考える必要があり、この場合も同様に手計算の方法を考えることに時間が取られてしまいますね。
手計算のプロでも複数の部材の検討、計算チェック作業に時間が取られるのは否めないのでCAEで検討しましょう。
また、人間の考えが及ばないと抜けや漏れが発生するリスクがあります。
部品に複雑な形状があり応力集中を考慮する必要がある
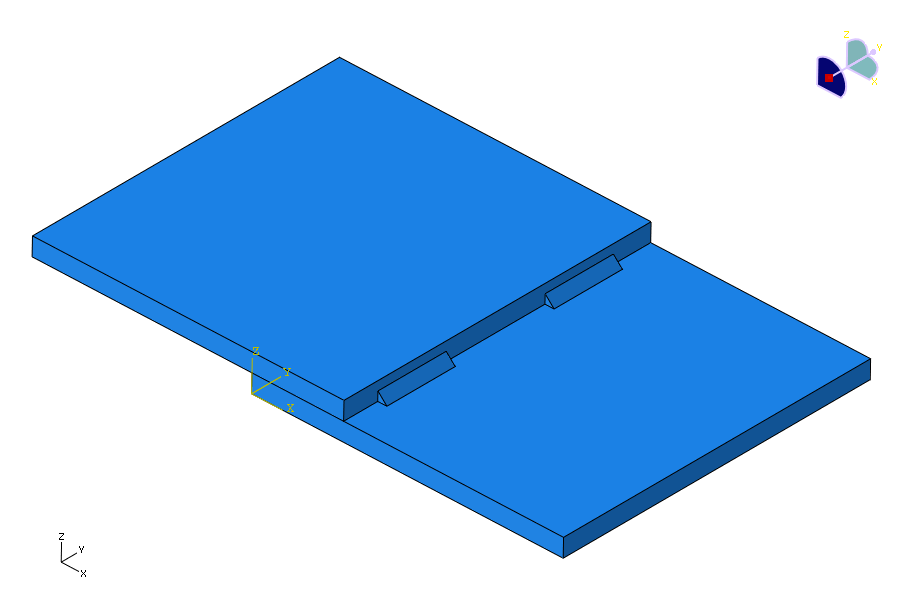
図12のように2枚のプレートが溶接接合されている場合、溶接部近傍の形状は複雑です(溶接を三角柱で表現しています)。
手計算では全く計算できないわけでは無いですが、手計算はプレート間の接触を考慮することもできず、必要以上に安全側な計算結果になることが予想されます。
このような場合、手計算に労力要する割に現実に近い結果が得られません。複雑な形状はCAEで検討し、別の重要なことに時間を活用しましょう。
まとめ
以上、設計にも活用できるCAE構造解析技術者の検証方法を解説しました。
上記に関連する内容でお困りごとがあればお問い合わせフォームに質問事項をご連絡頂ければ、時間があるときに回答させて頂きます。


