CAEの振動解析の妥当性の判断や手計算で固有振動数を推定することができるようになり、場合によっては不要な外注委託費用を削減し、必要なところに外注委託費用を回すことができます。
「今、CAEの外注委託先を考えはじめた」「今後CAEを設計に取り入れていこうと考えている」という方には「CAEの振動解析を外注委託するか否か」を考える上で参考になると思います。
「CAE受託ドットコム」は、CAE歴20年の管理人が自身の経験を元にCAEの有効な活用方法を発信するブログです。
下記に関連する内容でお困りごとがあれば下記ボタンのお問い合わせフォームに質問事項をご連絡頂ければ、時間があるときに回答させて頂きます。リクエストなどにも対応していきたいと思います。
CAEの振動解析で見るべき重要ポイント
振動解析で見るべき重要ポイントは下記の2つです。
- 固有振動数は何Hzか?
- 振動の変位の振幅は何mmか?
CAEの振動解析結果の妥当性を判断する上で、固有振動数、変位の振幅を事前に把握しておくことは重要です。これらを事前に把握することは測定結果があれば話は早いですが、そうでない場合これらを正確に予測することは難しいです(だからCAEを使っている)。しなしながら、これらの値をオーダー感を予測するという風にハードルを下げると、意外と簡単に予測できます。ここからは、誰もが簡単にできる固有振動数、変位の振幅の予測方法について解説していきます。設計する際の参考になる方もいると思うのでご興味がある方はぜひとも最後までお付き合い下さい。
固有振動数ってどうやって予測?
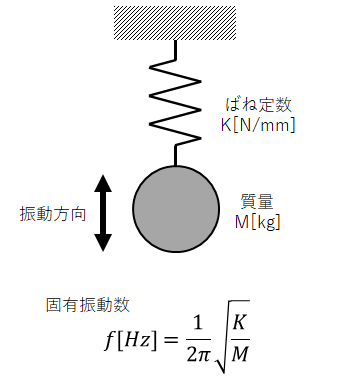
固有振動数の予測方法について解説します。高校物理では、質量M[kg]とばね定数K[N/m]を用いて固有振動数f[Hz]は、
f[Hz] = (1/2π)√(K/M)
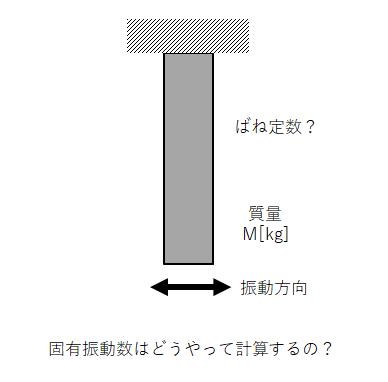
を勉強したと思います。この式は図2に示すように概念的に理解し易いですが、実際の構造物は図2に示すように質量Mは[kg]は分かるけど、左右方向の振動に対するばね定数が分からないという問題に直面します。ここでは、図2の固有振動数を簡単に求める方法について解説します。
- はりの曲げの固有振動数は計算式にあてはめれば簡単に計算できる
- 固定条件(ピン、固定、フリー)によって係数λが変わる
- 材質を選定(ヤング率E[MPa])
- はりの断面特性を選定(断面2次モーメントI[mm4]、断面積A[mm2])
- オーダー感を掴むという意識で大胆な近似
固有振動数の推定方法のポイントについて解説していきます。
はりの曲げの固有振動数は計算式にあてはめれば簡単に計算できる
はりの曲げの固有振動数は下記で簡単に計算できます。図1の式で言うと、EIがKに相当し、L2をルート内に入れると、ρALがMに相当する計算式になっています。単位系はmmのSI単位系を下記に記載します。
- 固有振動数f[Hz] = λn2/(2πL2) ×√(EI/ρA)
λn:固有振動数の係数[-]
L:はりの長さ[mm]
E:ヤング率[MPa]
I:断面2次モーメント[mm4]
ρ:密度[ton/mm3]
A:断面積[mm2]
この数式に値を代入するだけです。上記内容の出典元は下記です。機械工学便覧は様々な出典元として活用でき、辞書代わりに多くの場面で活用できるのでお持ちでない方はにおすすめです。
では実際に図3を例に固有振動数を算出してみましょう。固有振動数λnは別途解説します。断面2次モーメントは【強度解析は手計算でできる?】手計算の使いどころを考えたCAE構造解析の検証方法にも記載していますが、手計算も面倒な場合はCADソフトに算出してもらうのが一番手っ取り早く、ミスも減らせると思います。エクセル上で断面形状を色々と検討したい場合は、断面2次モーメントを手計算で計算できるようになる必要があります。今後、断面2次モーメントの計算方法についても発信する予定です。
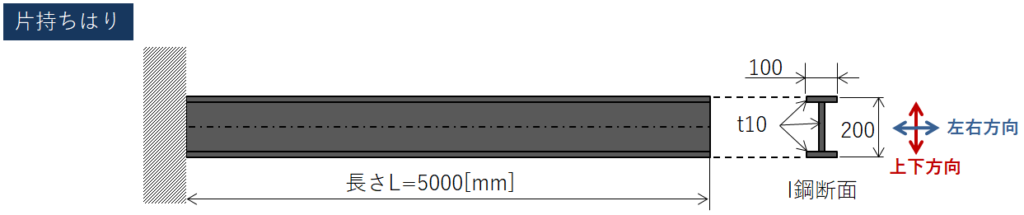
はりの曲げの固有振動数は上記の計算式で簡単に計算できました。固有振動数の係数λnは固定条件によって変わってくるので、次に固定条件とλnとの関係性について解説します。
固定条件(ピン、固定、フリー)によって係数λが変わる
- フリー~フリー λ1=4.730、λ2=7.853、λ3=10.996
- ピン~ピン λ1=π、λ2=2π、λ3=3π
- ピン~フリー λ1=3.927、λ2=7.069、λ3=10.210
- 固定~ピン λ1=3.927、λ2=7.069、λ3=10.210
- 固定~フリー λ1=1.875、λ2=4.694、λ3=7.855
- 固定~固定 λ1=4.730、λ2=7.853、λ3=10.996
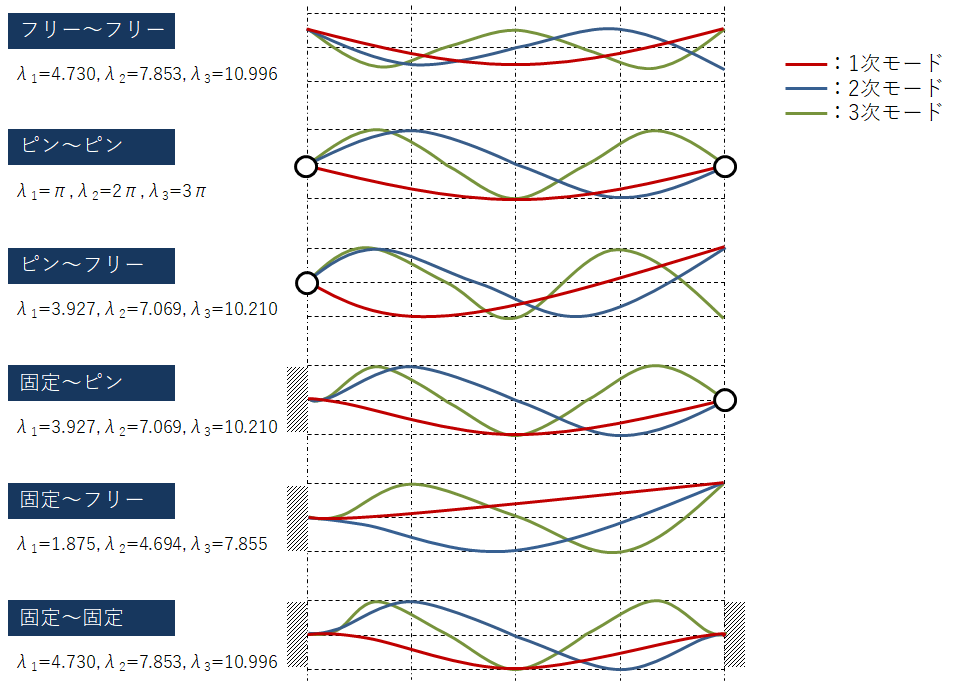
上記のようにはりの固定条件によってλnが変わり、はり曲げの固有振動モードもそれぞれ異なります。設計する上で注意が必要なのは1次モードだと思いますのでλ1を固有振動数の係数としてご活用下さい。場合によっては、2次や3次モードも必要になるかと思いますのでその際はλ2、λ3を用いて固有振動数を計算して頂ければと思います。
材質
材料の硬さを示すパラメータのヤング率Eと密度ρは、下記を参考にして下さい。今回は炭素鋼を例に上記で計算しました。
- 炭素鋼(SS400など):E=206,000[MPa]、密度ρ=7.85×10-9[ton/mm3]
- ステンレス鋼(SUS304):E=193,000[MPa]、密度ρ=7.93×10-9[ton/mm3]
- 純アルミ(A1085):E=69,000[MPa]、密度ρ=2.7×10-9[ton/mm3]
- アルミ合金(A2024):E=74,000[MPa]、密度ρ=2.77×10-9[ton/mm3]
オーダー感を掴むための大胆な近似
実際の構造物は、上記のような条件に必ずしもあてはまらず下記のような場合が多いです。
- はり断面が一様断面ばかりでは無い
- 固定部が固定とピン支持の間のような支持条件
条件が違えば全く予測できないかと言えばそうではありません。CAEの精度検証を行う上で重要なことは、オーダー感が合っていることを確認することです。下記の事例について手計算とCAEの結果と比較してみましょう。
固有振動数の検証
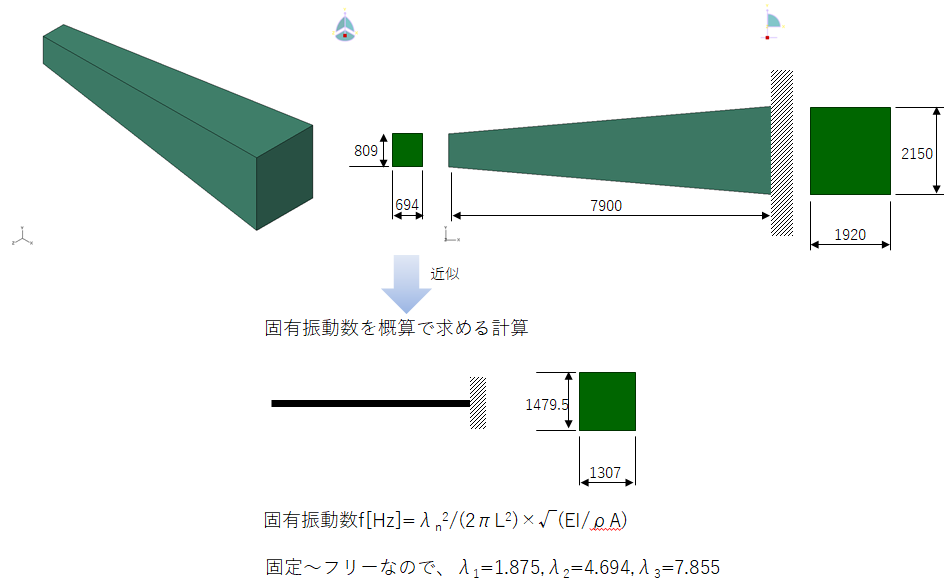
図5に示すはりの断面形状が固定部から先端へ連続的に変化する片持ちはりの固有振動数を手計算で概算します。ここで重要なのは短時間でCAEの結果のオーダー感の検証する、あるいは振動設計において最適な形状を検討することなのでたわみ量の計算は、図5に示すような近似を行います。片持ちはりの固有振動モードは、図4に示すようにはり全体が変形します。したがって、近似する断面は固定部と先端の平均断面とします。では、実際に近似した片持ちはりの固有振動数を計算してみます。
- はりの断面を一様断面に近似
- 近似する一様断面は、はり全体の平均断面を使う
上記は1次モードについて計算してみました。続いて、2次モードについても同様に計算してみます。
ここで注意したいのはこの数値は、平均的な一様断面の計算結果であるため、下記理由により実際の固有振動数は左右方向の17.3[Hz]より高くなるはずであるという点です。
- 実際の断面形状は、はり固定部が太く、先端が細い
→近似したはりよりも変形が小さい→実際は近似したはりより固有振動数は高くなるはず
次にFEMの計算をしてみます。境界条件は、はりの固定部のみを拘束しました(図6参照)。図7から図10にCAEの固有振動数解析結果を示します。
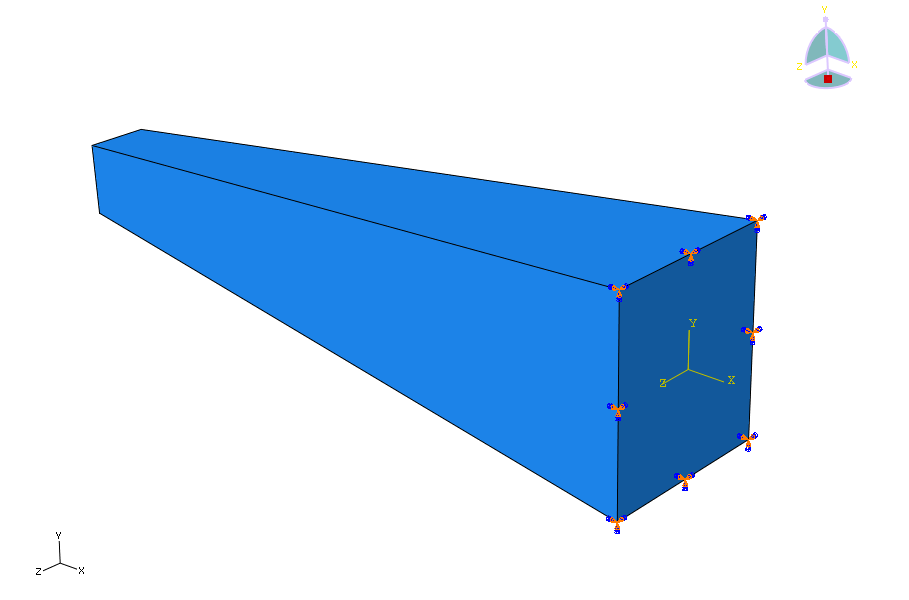




表1に手計算とCAEの固有振動数を比較した結果を示します。
| 固有振動数 手計算[Hz] | 固有振動数 CAE[Hz] | |
| 左右曲げ(1次モード) | 17.3 | 34.9 |
| 左右曲げ(2次モード) | 109 | 117 |
| 上下曲げ(1次モード) | 19.6 | 39.4 |
| 上下曲げ(2次モード) | 123 | 129 |
手計算とCAEの結果から、
- 手計算とCAEのオーダー感は一致している
- 手計算より、CAEのほうが固有振動数が高い
ということが分かり、CAEの結果が妥当であると判断できます。このように大胆な近似を行うことでCAEの妥当性を判断できるので皆さんもぜひご活用してみてください。エクセルで計算式作ってしまえばCAEで検討するより効率的に設計が進むと思います。
振動の変位の振幅は何mmか?
振動を抑えた設計をするためのもう一つの重要な要素は、構造物の振動の変位の振幅が何mmになるのかを知ることだと思います。変位の振幅が分かれば発生応力が予測でき、強度が担保できるか判断できますからね。
ですが、手計算では振動の変位の振幅を正確に予測することは非常に難しいです。
その理由は、
- 振動の加振源の周波数が構造物の固有振動数に近く、共振の影響を受けることが多い
- 構造物の減衰を設計段階で正確に把握することは困難(摩擦で減衰が大きく変わる)
であるからです。とは言え、オーダー感を掴む程度でよければ簡単に予測可能です。ここからは、その方法について解説していきます。振動の変位の振幅は、分かっている情報によって算出のアプローチ方法が変わってくるので以下のケースについて考えていきます。
- 実測値などの加速度の情報がある場合
- 実測値の加速度の情報がない場合
- 手計算で振動の変位の振幅を正確に予測することは非常に難しい
- 振動の変位の振幅のオーダー感を掴むことは容易
- 実測値の加速度がある場合と無い場合でアプローチは変わる
振動の変位の振幅を簡単に予測する方法~加速度が既知の場合~
最も変位が大きくなると予想される箇所の加速度が実測等で分かっている場合は、下記の式で簡単に計算することが可能です。
- 変位u[mm] = a/ω2
a[mm/s2]:実測値などの最も変位が大きくなると予想される箇所の加速度
角振動数ω[rad/s] = 2πf
f[Hz]:振動数
例えば、構造物の共振周波数の変位量が知りたい場合、fに固有振動数を入力すると、構造物が固有振動数で振動した際の変位を概算することができます。さらに、加振源の周波数の変位量が知りたい場合、fに加振周波数を入力すると、構造物が加振周波数で振動した際の変位を概算することができます。
加速度が既知の場合は、このような方法で簡単に計算することが可能です。ただし、既知の加速度は実測値を使うようにしてください。実測値では無く計算値の場合は、減衰が適切でないと計算精度が著しく低下する可能性があります。また、変位が最大となる箇所の予測が難しい場合は、CAEでの検討を推奨します。
振動の変位の振幅を簡単に予測する方法~加速度が未知の場合~
次に、こちらのケースのほうが圧倒的に多いと思われる加速度が未値の場合の振動の変位の振幅を簡単に予測する方法について解説します。加速度が既知の場合に比べて少しだけ複雑になりますが、下記に示す振幅倍率Mの式で簡単に計算することが可能です。
- 振幅倍率M[-] = X/Xst = 1/√{1-(ω/ωn)2}2+{2ζ(ω/ωn)}2
X[mm]:構造物の振動の振幅
Xst[mm]:加振源の振動の振幅
ζ[-]:減衰比
ω[rad/s]:加振源の角振動数(=2πf)
ωn[rad/s] :構造物の固有角振動数(=2πfn)
f[Hz]:加振源の振動数
fn[Hz]:構造物の固有振動数
上記内容の出典元は下記です。振動工学の書籍は慣れるまでに時間がかかりますが、下記の書籍は非常に初心者に分かりやすく書かれているのでおすすめです。また、振動計測のことについても書かれており、実用性の高い書籍です。
振動の変位の振幅を簡単に予測する方法~検証編~
振動の変位の振幅を予測する方法について解説したので実際に手計算とCAEを検証してみたいと思います。図11に示すような両端ピン支持の両端を±100[mm]で4[Hz]、5.333[Hz]、8[Hz]の3条件違いで加振した際の中央部の変位量を計算してみたいと思います。はりは、直径2[mm]の丸棒で1次の固有振動数は4[Hz]です。加振周波数は、丸棒の固有振動数と一致する4[Hz]、丸棒の固有振動数+33%とした5.333[Hz]、丸棒の固有振動数+100%とした8[Hz]の3条件で検討します。このような解析は周波数応答解析と呼びます。
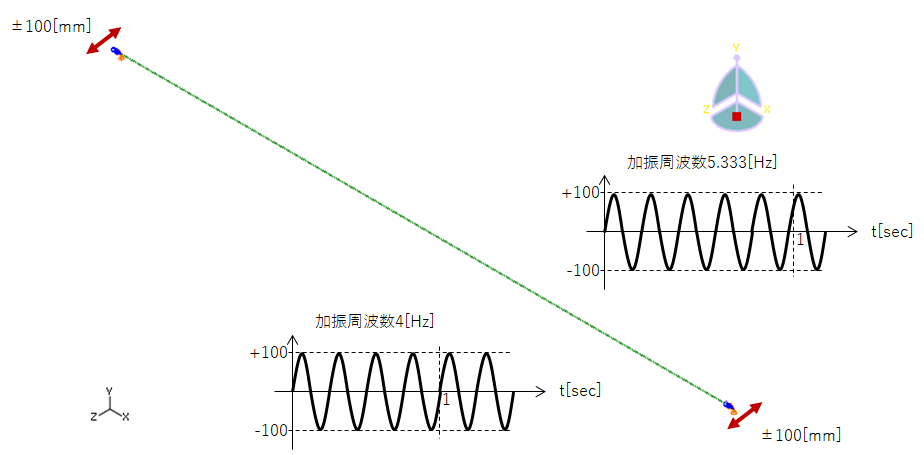
図12から図14に4,5.333,8[Hz]で両端を±100[mm]で加振したときの振動の様子を示します。図12の丸棒の固有振動数で加振した場合(共振させた場合)、端部±100[mm]に対して中央がかなり大きく振れていることが分かります。実物だったら即効で壊れるレベルです。
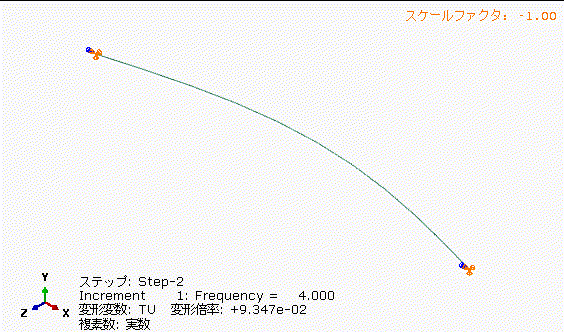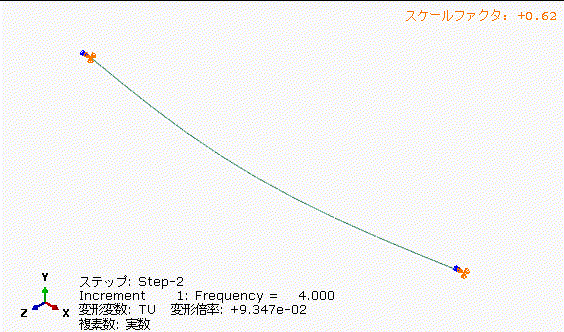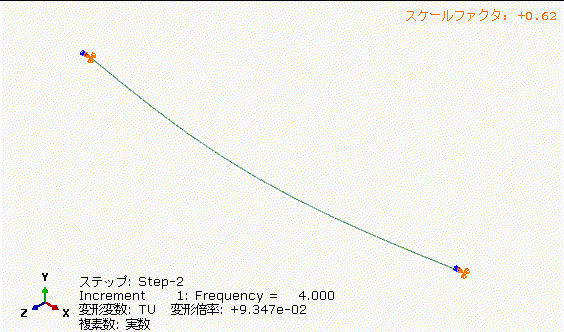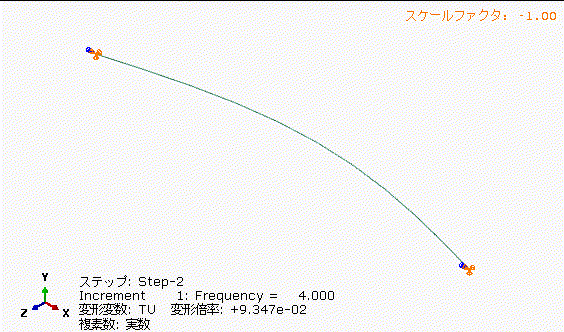
図13の丸棒の固有振動数+33%で加振した場合、図12の4[Hz]加振に比べて、中央部の振れ量が小さくなっています。共振周波数を少し外すだけでもかなり振れ量低減できますね。
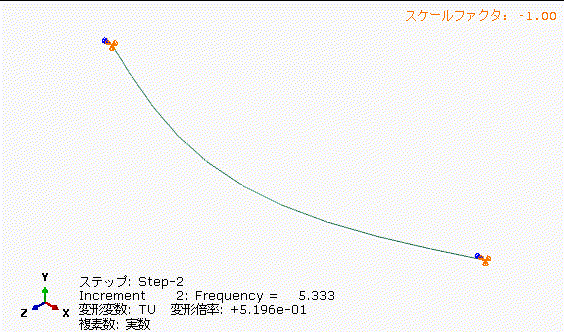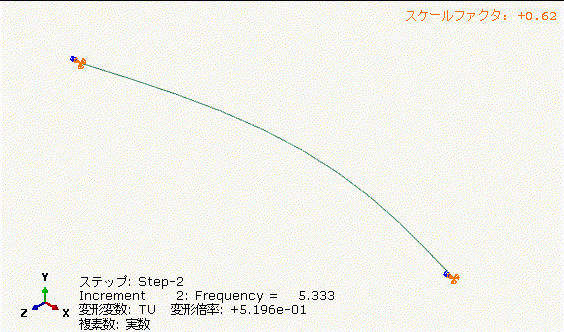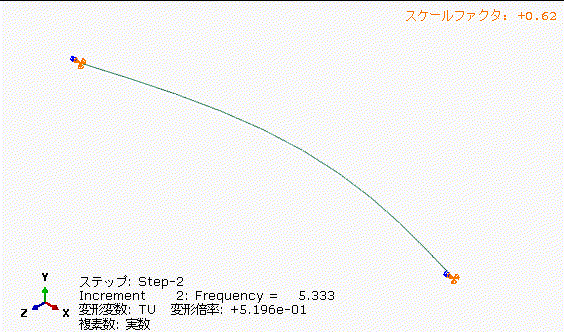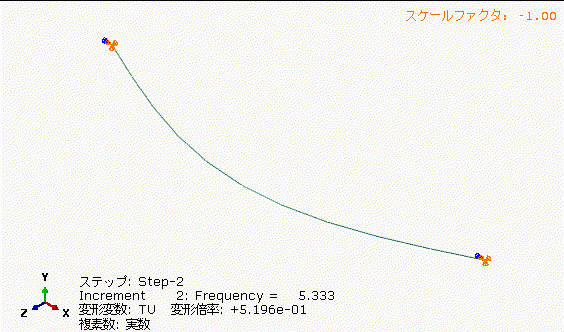
図14の丸棒の固有振動数+100%で加振した場合、図13の5.333[Hz]加振に比べて、さらに中央部の振れ量が小さくなっています。加振周波数と固有振動数を離してあげることは重要ですね。
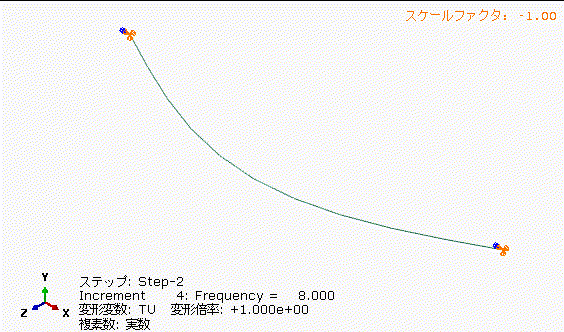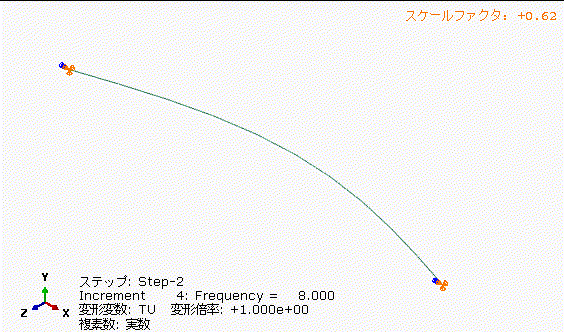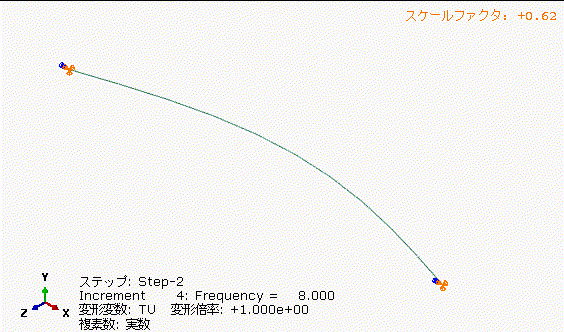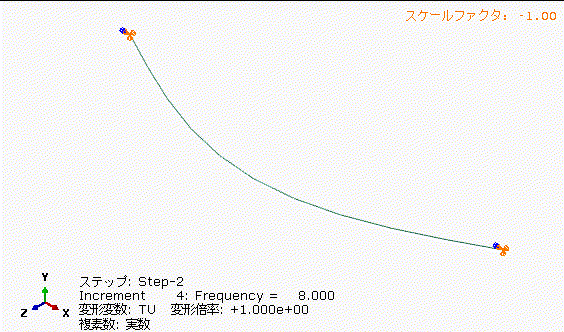
表2に図12から図14のはり中央部の変位量、加速度の振幅をまとめました。
| 変位量[mm] | 加速度[m/s2] | |
| 加振周波数4[Hz] | 2996 | 1893 |
| 加振周波数5.333[Hz] | 194 | 217 |
| 加振周波数8[Hz] | 69 | 175 |
次は、CAEと同じ計算を上記で説明した手計算で計算してみましょう。
加速度が分かっている場合の丸棒の変位量を手計算で算出しました。表2に示したCAEの結果と完全に一致しています。加速度が分かっている場合、振動の振幅を算出することは簡単ですね。
次は、加速度が分かっていない場合の丸棒の変位量を手計算で算出してみます。
表3にCAEと手計算の変位量を比較しました。加速度が既値の場合は、当然のようにCAEの結果と一致します。加速度が未知の場合でもそれなりの精度で計算できていることが確認できます。以上、変位量のオーダー感を掴むという目的であれば、簡単な計算式で変位量が計算できることがお分かり頂けたかと思います。
| CAE変位量[mm] | 手計算変位量[mm] 加速度が既知 | 手計算変位量[mm] 加速度が未知 | |
| 加振周波数4[Hz] | 2996 | 2996 | 2414 |
| 加振周波数5.333[Hz] | 194 | 194 | 131 |
| 加振周波数8[Hz] | 69 | 69 | 34 |
変位量のオーダー感を掴む目的であれば手計算で十分なことも多いです。しかしながら、振動の発生応力から疲労寿命を予測したいとなった場合は、変位量を正確に予測できなければ発生応力を正しく予測することができません。そのような場合は、手計算は諦めてCAEで検討することをおすすめします。
まとめ
以上、設計にも活用できるCAE振動解析技術者の検証方法を解説しました。
- はりの曲げの固有振動数は下記の計算式にあてはめれば簡単に計算できる
固有振動数f[Hz] = λn2/(2πL2) ×√(EI/ρA)
λn:固有振動数の係数[-]
L:はりの長さ[mm]
E:ヤング率[MPa]
I:断面2次モーメント[mm4]
ρ:密度[ton/mm3]
A:断面積[mm2] - 固有振動数の推定方法のポイント
オーダー感を掴むという意識で大胆な近似が重要
加振周波数と固有振動数は十分に離してあげることが重要 - 振動の変位の振幅は以下の方法で計算できる
加速度が既知の場合
変位u[mm] = a/ω2
a[mm/s2]:実測値などの最も変位が大きくなると予想される箇所の加速度
角振動数ω[rad/s] = 2πf
f[Hz]:振動数
加速度が既知の場合
振幅倍率M[-] = X/Xst = 1/√{1-(ω/ωn)2}2+{2ζ(ω/ωn)}2
X[mm]:構造物の振動の振幅
Xst[mm]:加振源の振動の振幅
ζ[-]:減衰比
ω[rad/s]:加振源の角振動数(=2πf)
ωn[rad/s] :構造物の固有角振動数(=2πfn)
f[Hz]:加振源の振動数
fn[Hz]:構造物の固有振動数 - 手計算の適用範囲
CAEの結果の妥当性確認
設計検討段階の簡易的な評価(疲労評価などでの活用は危険)
上記に関連する内容でお困りごとがあれば下記ボタンのお問い合わせフォームに質問事項をご連絡頂ければ、時間があるときに回答させて頂きます。リクエストなどにも対応していきたいと思います。




