構造物の設計において、外部、あるいは内部から何かしらの振動が入力される場合、一番に考えるべきことはその構造物が外部、あるいは内部の振動に対して共振するか否かです。それを判断するためにCAEで固有振動数解析をします。CAEで計算した固有振動数が設計構造物に入力される振動の周波数と一致するか否かを判断するだけですね。簡単です。ただ、入力される振動の周波数に対して、固有振動数がどの程度離れていれば共振を回避できるのか?という疑問をお持ちになる方もいると思います。そんな方のために参考になる記事を書いてみようと思います。
「CAE受託ドットコム」は、CAE歴20年の管理人が自身の経験を元にCAEの有効な活用方法を発信するブログです。
下記に関連する内容でお困りごとがあれば下記ボタンのお問い合わせフォームに質問事項をご連絡頂ければ、時間があるときに回答させて頂きます。リクエストなどにも対応していきたいと思います。
固有振動数は何に役立つのか?共振はどうやって回避する?
- 固有振動数解析は意外と役に立ち、他の解析よりコストが安い
- 構造物の固有振動数を知ることで疲労破壊防止に役立つ
- 構造物の固有振動数を知ることで不快音の発生の防止に役立つ
- 共振回避は応答倍率で考える
詳細が知りたい方は↓を参考にして下さい。
CAEで費用をかけて固有振動数解析をする必要はあるのか?
本題に入る前に、そもそもCAEで費用をかけて固有振動数解析をする必要があるのかどうかについて解説します。結論を言うと、
- 手計算で固有振動数を計算できるものはCAEをやる必要がない
- ハンマリング試験で実物を試験できるものはCAEをやる必要がない
- 手計算で計算できず、実物が無い設計品についてはCAEをやったほうが良い
といった感じです。1から3についてそれぞれ解説します。
1.については、時間・労力、費用から言うまでもないですね。手計算の方法について知りたい方は【固有値解析って手計算でできる?】共振について考える振動解析の検証方法に固有振動数を手計算で計算する方法について記載しているので参考にしてください。
2.については、実物があるのであればそれを計測するのが一番ですね。構造物に加速度ピックアップを設置し、インパルスハンマで打撃すれば固有振動数が分かります。CAEはあくまで机上の計算なのでモデル化方法によっては全く実物を再現できない場合もあります。構造物同士の接触が多く、接触状態が不明瞭な場合はCAEの予測精度に疑問点が残ります。そういう場合は特にハンマリング試験をやっておきたいですね。
3.の場合、諦めてCAEで固有振動数解析をやらなければなりません。共振が疲労破壊を引き起こす可能性は大いにあります。回転機械などは破損が事故にも繋がるので必ず固有振動数を確認しておきましょう。ハンマリング試験ができない場合、CAEのモデルは固有振動数が低くなる側にモデル化し、設計する際は、固有振動数が加振周波数を超えるように設計することをおすすめします。
固有振動数解析はコスパ最強
固有振動解析はコスパ最強なので、活用されていない方はぜひ活用してみてください。固有振動数解析は固有振動数を求める解析ですが、その固有振動数における振動(変形)モードを再現できるメッシュ分割であれば良いので解析ソフトのオートメッシュでも十分です。固有振動数は基本的には質量、剛性、境界条件で決まるので減衰なども考える必要は無く、さらには入力加振力なども不要です。したがって、解析者の作業量も少ないため応力解析、振動解析(周波数応答解析、時刻歴応答解析など)よりコストは下げられます。
固有振動数解析はどういう場合に使うの?
固有振動数解析の活用事例をご紹介します。
事例① 配管の共振

一般的に配管は、液体、気体などの流路となるため、ポンプを使って流体が配管内を流れます。その場合、配管はポンプなどの回転機器に接続されているため、回転機器や配管内部の流体の圧力変動によって加振されます。
例えば、回転機器は重量のアンバランス、軸芯からのミスアライメントにより、回転機器の回転数[rpm]に応じた加振周波数で加振されます。この場合、加振周波数f[Hz]=n・回転数N/60で計算されます。nは整数。
往復圧縮機では、ピストンの動きに応じて流体を吸引・吐出するため、圧力変動が発生し、ピストン数と回転数に応じた加振周波数で加振されます。この場合、加振周波数f[Hz]=n・ピストン数P・回転数N/60で計算されます。nは整数。
遠心圧縮機では、ブレードの羽の動きに応じて流体を圧縮するため、圧力変動が発生し、ブレードの羽の枚数と回転数に応じた加振周波数で加振されます。この場合、加振周波数f[Hz]=n・羽の枚数B・回転数N/60で計算されます。nは整数。
となると、ポンプなどの回転機器に接続される配管は、ポンプなどの回転機器との共振を回避する必要がありますね。このような場合、配管の固有振動数を計算し、上記の加振周波数と配管の固有振動数を一致させないことで共振を回避できます。
ここでは簡単な配管の事例を取り上げて固有振動数をCAEで計算してみます。

ポンプの接続部はピン支持、支持サポート部は配管軸方向以外の並進方向を拘束して固有振動数解析をしてみます。




ここで、仮に遠心圧縮機のポンプの回転数が3000[rpm]でポンプ内の羽の枚数が8枚とした場合、ポンプの圧力変動による加振周波数f[Hz]は、f=8×3000/60=400[Hz]となります。
そうなると、4番目の振動モードと共振する可能性があるということになります。
この場合は、支持サポートを増加するなどの対策が必要ですね。試しに支持サポートを追加する検討などはCAEであっという間に検討することが可能です。
事例② 薄板の共振

薄板は、写真にあるように自動車をはじめ、プラント設備など様々なところで活用されます。
自動車のように路面走行からの広範囲の加振周波数を考慮しなければならないケースもあれば、プラント設備内に設置された鋼板に流体の圧力変動が作用し、ある加振周波数で加振されるようなケースもあります。
ここでは簡単な薄板の事例を取り上げて固有振動数をCAEで計算してみます。

左側は少しアーチ型の形状のあるt1.0の鋼板、右側は完全にフラットのt1.0の鋼板です。
どちらも材質、幅1000[mm]、長さ1000[mm]、厚み1[mm]です。
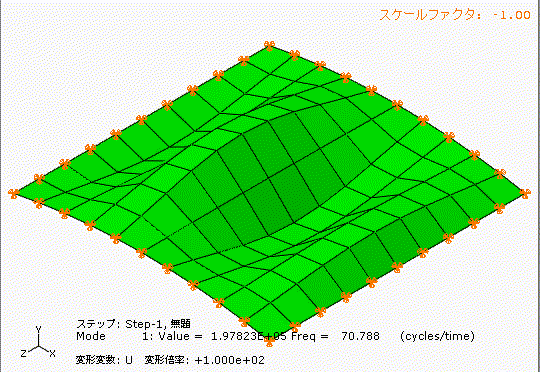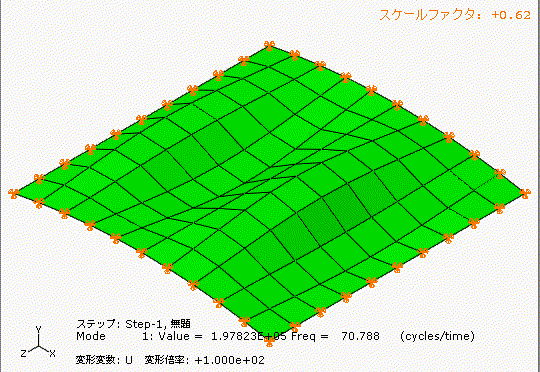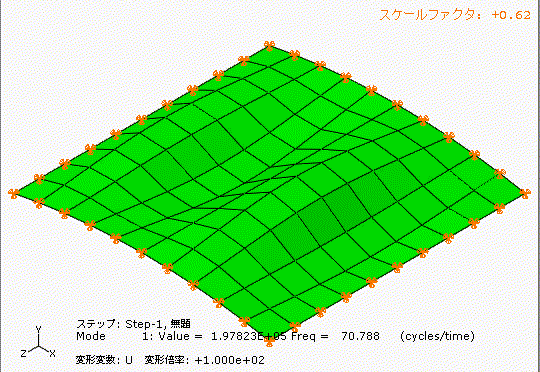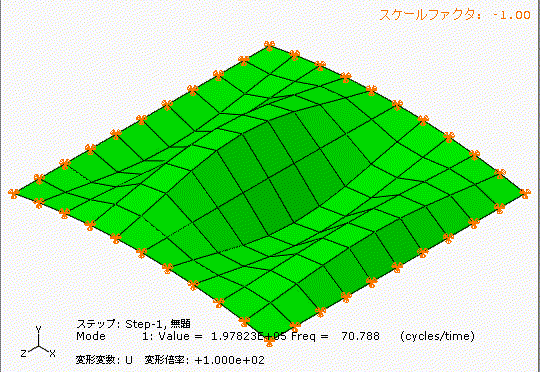

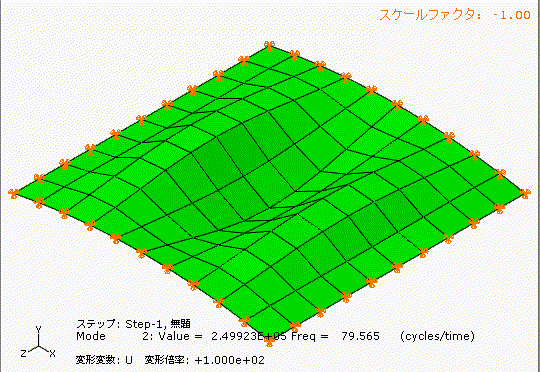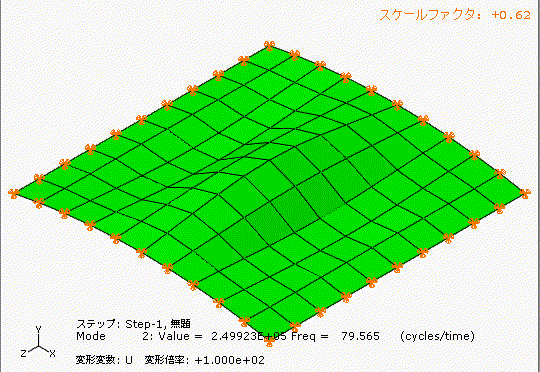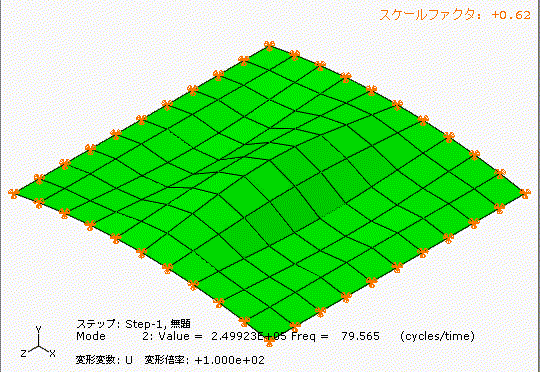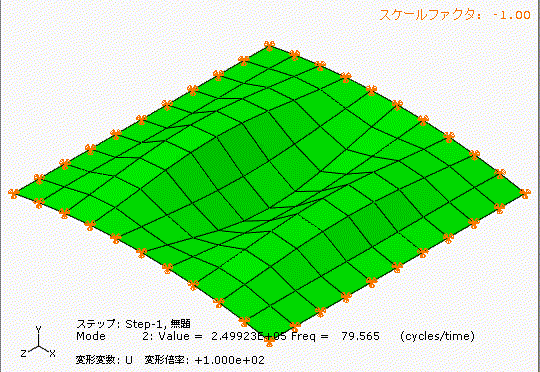
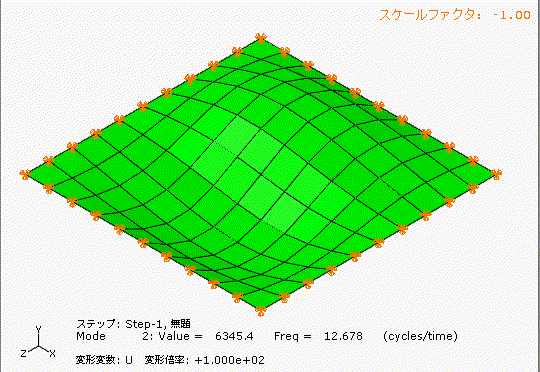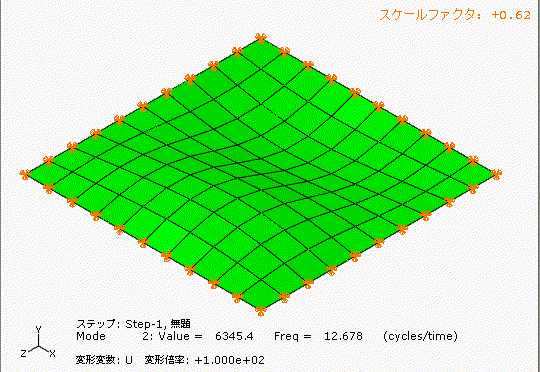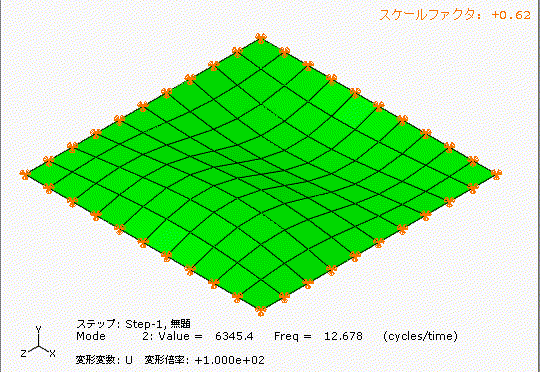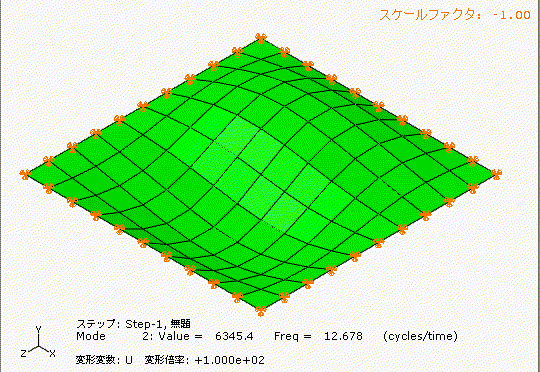
アーチ状の薄板と完全平板では、固有振動数が全く違いますね。フープテンションの力は凄い。
薄板円筒は面外方向に変形しようとすると、円周方向に引っ張られて踏ん張ってくれます。
したがって、薄板構造の固有振動数は注意が必要です。アーチ形状を完全平板に置き換えて手計算で検討すると痛い目を見ます。
薄板構造に形状がある場合も同様に注意が必要です。
ここで、仮に往復圧縮機が4気筒で1000[rpm]だった場合、加振周波数f[Hz]はf=4×1000/60=67[Hz]となり、アーチ状の薄板の1次の固有振動数(71Hz)と共振する可能性があることが分かります。
事例③ 鋳造、削り出し部品などの共振

配管、薄板だけで無く鋳造、削り出し部品などの構造物も固有振動数があります。
鋳造などの比較的厚みのある構造物は固有振動数が高く、共振による疲労破壊の心配は少ないかもしれません。
一方、固有振動数が高い部品で問題となるケースに騒音問題があります。人間の可聴周波数帯域は20Hz~20,000Hzと言われていますが、その中でも2,000Hz~4,000Hzの音を人間は不快に感じるそうです。
音の発生は構造物が空気を振動させてそれが空気中を伝搬し、人間の鼓膜を振動させています。
したがって、仮に鋳造の構造物の固有振動数が2,000Hz~4,000Hzの間にあると、不快な音の発生源になる可能性があります。
ただし、構造物の固有振動数が3,000Hzだとしても加振源が2,000Hz~4,000Hzの間に全く無ければ3,000Hzで振動することは無いので問題になることはありません。
ここでは簡単な球体バルブ状の構造物の事例を取り上げて固有振動数をCAEで計算してみます。
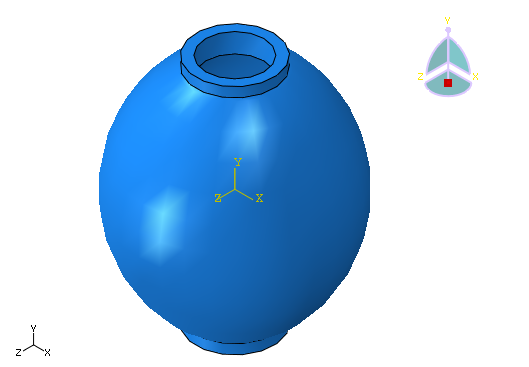

このケースでは、球体バルブ状の固有振動数は1,186Hzと周波数は高くなりました。
もしも高い音の騒音が問題になった場合は、このように固有振動数の高そうな構造物が原因かもしれませんね。
共振を回避するにはどうしたら良い?
共振を回避するためには、加振周波数と構造物の固有振動数を一致させなければ良いということは分かっていますが、これらがどの程度離れていると安全と判断できるのでしょうか。
この判断材料となるのが下記の応答倍率です。共振応答倍率と静的変位が分かることにより応答変位を推定することができます。応答変位が分かれば、加振周波数で加振された際の発生応力が分かり、安全か危険かどうかの判定をすることができます。

応答倍率Mは、全く共振の影響を受けない場合の静的変位に対して、共振の影響のある周波数帯域で加振すると変位が何倍になるのかを意味します。
応答倍率Mについては、下記の書籍が参考になります。振動の基礎から実用的なところまで記載されているのでお勧めの書籍です。
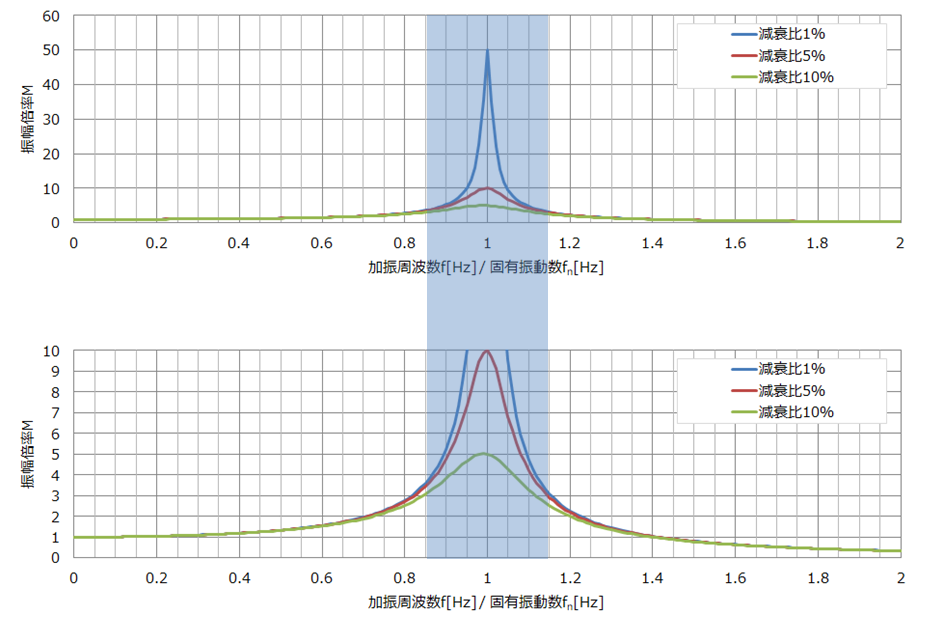
応答倍率Mを横軸を加振周波数/固有振動数としてグラフにしてみました(下記グラフ)。
材質によって減衰比が異なるため、金属材料を想定した減衰比1%、樹脂材料を想定した減衰比5%、ゴム材料を想定した減衰比10%の3種類示します。
f/fn=1のとき、固有振動数と加振周波数が一致した際の応答倍率です。減衰比毎の応答倍率Mは、
- 減衰比1%:50倍
- 減衰比5%:10倍
- 減衰比10%:5倍
減衰比1%の場合は、変形が50倍になるということなので金属材料の共振は危険です。
一方、減衰比10%の場合は、変形が5倍程度で収まるのでゴム材料だと比較的安心です。
応答倍率Mのグラフが理解できたと思いますので、次は共振回避の方法について考えていきましょう。

例えば、加振周波数と固有振動数を5%離した場合を考えます(上図のグラフの青の範囲)。
加振周波数と固有振動数を5%離した場合の応答倍率Mは、
- 減衰比1%:10倍(←50倍)
- 減衰比5%:7倍(←10倍)
- 減衰比10%:4.5倍(←5倍)
加振周波数と固有振動数を5%離すだけで応答倍率Mは激減しますね。ただし、応答倍率Mはまだまだ大きいです。

次は、加振周波数と固有振動数を10%離した場合を考えます(上図のグラフの青の範囲)。
加振周波数と固有振動数を10%離した場合の応答倍率Mは、
- 減衰比1%:5倍(←50倍)
- 減衰比5%:4.5倍(←10倍)
- 減衰比10%:3.5倍(←5倍)
加振周波数と固有振動数を10%離すと応答倍率Mはさらに下がります。ここまでくると減衰比による差異がかなり小さくなってきますね。
次は、加振周波数と固有振動数を15%離した場合を考えます(上図のグラフの青の範囲)。
加振周波数と固有振動数を15%離した場合の応答倍率Mは、
- 減衰比1%:3.4倍(←50倍)
- 減衰比5%:3.4倍(←10倍)
- 減衰比10%:3.0倍(←5倍)
加振周波数と固有振動数を15%離すと応答倍率Mはさらに下がります。ここまでくると減衰比による差異がほとんど無くなります。

ここまで共振回避を行うために固有振動数を加振周波数から何%離せば良いかを考えましたが、共振の影響をゼロにすることは難しいことが理解できたと思います。
したがって、現実的には応答倍率Mを下げると同時に静的変位を下げながら応答変位を下げていくことが良いと思います。
固有振動数解析ではここまでしか検討できませんが、周波数応答解析を行えば一度に共振時の発生応力まで求めることが可能です。
周波数応答解析についてまたの機会に解説したいと思います。
まとめ
- CAEで費用をかけて固有振動数解析をする必要はあるのか?
手計算で固有振動数を計算できるものはCAEをやる必要がない
ハンマリング試験で実物を試験できるものはCAEをやる必要がない
手計算で計算できず、実物が無い設計品についてはCAEをやったほうが良い - 固有振動数解析はコスパ最強
メッシュ分割は解析ソフトのオートメッシュで十分
解析者の作業量も少ないためコストは下げられる - 固有振動数は加振周波数とどの程度離せば安全?
応答倍率Mと静的変位から応答変位を推定することで安全かどうかを判断できる
周波数応答解析を行えば、一度に共振時の発生応力まで計算でき安全性を判断可能
上記に関連する内容でお困りごとがあれば下記ボタンのお問い合わせフォームに質問事項をご連絡頂ければ、時間があるときに回答させて頂きます。リクエストなどにも対応していきたいと思います。